Correlazione (statistica)
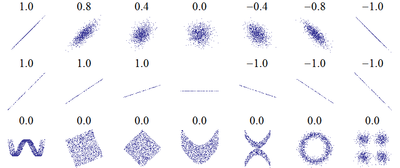
In statistica, una correlazione è una relazione tra due variabili tale che a ciascun valore della prima corrisponda un valore della seconda, seguendo una certa regolarità.[1][2] La correlazione non dipende da un rapporto di causa-effetto quanto dalla tendenza di una variabile a cambiare in funzione di un'altra.
Detto altrimenti correlazione non significa causazione[3].
Storia
[modifica | modifica wikitesto]Il termine apparve per la prima volta in un'opera di Francis Galton, Hereditary Genius (1869).[4] Non fu definita in modo più approfondito (la moralità di un individuo e la sua instabilità morale sono non correlate)[5].
Otto anni dopo, nel 1877, lo stesso Galton scoprì che i coefficienti di regressione lineare tra X e Y sono gli stessi se a entrambe le variabili viene applicata la deviazione standard σx e σy: Galton utilizzò in realtà lo scarto interquartile, definendo il parametro "coefficiente di co-relazione" e abbreviando "regressione" in r[6].
Descrizione
[modifica | modifica wikitesto]In base alle caratteristiche presentate, la correlazione può definirsi:
- diretta (o positiva): la variazione di un elemento interessa - in via diretta - anche l'altro. Per esempio, alle stature alte dei padri corrispondono stature alte dei figli;
- indiretta (anche inversa o negativa): alla variazione di un elemento corrisponde, in senso contrario, quella dell'altro. Ad esempio, a una maggior produzione di grano corrisponde un prezzo minore.
Inoltre, le correlazioni possono essere:
- semplici: mettono in relazione due fenomeni, per esempio il numero di matrimoni e la quantità di nascite;
- doppie: se i fenomeni posti in relazione sono tre, come la circolazione monetaria, i prezzi e il risparmio;
- triple: quando pongono in relazione tra loro quattro elementi.
Il grado di correlazione tra due variabili viene espresso tramite l'indice di correlazione.[7] Il valore che esso assume è compreso tra −1 (correlazione inversa) e 1 (correlazione diretta e assoluta), con un indice pari a 0 che comporta l'assenza di correlazione; il valore nullo dell'indice non implica, tuttavia, che le variabili siano indipendenti.
I coefficienti di correlazione sono derivati dagli indici, tenendo presenti le grandezze degli scostamenti dalla media. In particolare, l'indice di correlazione di Pearson è calcolato come rapporto tra la covarianza delle due variabili e il prodotto delle loro deviazioni standard:[8]
Va comunque notato che gli indici e i coefficienti di correlazione siano da ritenersi sempre approssimativi, a causa dell'arbitrarietà con cui sono scelti gli elementi: ciò è vero, in particolare, nei casi di correlazioni multiple.
Contrariamente a quanto si potrebbe intuire, la correlazione non dipende da un rapporto di causa-effetto quanto dalla tendenza di una variabile a cambiare in funzione di un'altra.[9] Le variabili possono essere tra loro dipendenti (per esempio la relazione tra stature dei padri e dei figli) oppure comuni (relazione tra altezza e peso di una persona).[10]
Nel cercare una correlazione statistica tra due grandezze, per determinare un possibile rapporto di causa-effetto, essa non deve risultare una correlazione spuria.[11]
Errore standard
[modifica | modifica wikitesto]Se e sono variabili aleatorie, l'errore standard associato al coefficiente di correlazione è:
dove è il coefficiente di correlazione e è la numerosità campionaria.[13][14]
Note
[modifica | modifica wikitesto]- ^ Definizione di correlazione, su dizionari.corriere.it. URL consultato l'8 ottobre 2017.
- ^ Paolo Enriques, Filippo Bottazzi e Giorgio Mortara, CORRELAZIONE, su treccani.it, 1931.
- ^ https://www.tylervigen.com/spurious-correlations
- ^ La nascita del concetto di correlazione (PDF), su padis.uniroma1.it. URL consultato il 23 gennaio 2018 (archiviato dall'url originale il 25 luglio 2018).
- ^ (EN) Francis Galton's account of the invention of correlation, su jstor.org, maggio 1989.
- ^ Regressione, su treccani.it. URL consultato il 18 giugno 2018.
- ^ Indice di correlazione, su alcula.com.
- ^ Dove si semplificano i fattori a numeratore e denominatore.
- ^ Il concetto di correlazione (PDF), su pellerey.unisal.it. URL consultato il 22 gennaio 2018.
- ^ Analisi di correlazione (PDF), su sisdin.unipv.it. URL consultato il 26 novembre 2017.
- ^ Correlazione [collegamento interrotto], su albanesi.it. URL consultato il 2 giugno 2018.
- ^ Slides Chignola Statistica (PDF), su profs.sci.univr.it.
- ^ A. L. Bowley, The Standard Deviation of the Correlation Coefficient, in Journal of the American Statistical Association, vol. 23, n. 161, 1928, pp. 31–34, DOI:10.2307/2277400, ISSN 0162-1459.
- ^ Derivation of the standard error for Pearson's correlation coefficient, su Cross Validated. URL consultato il 21-07-30.
Voci correlate
[modifica | modifica wikitesto]- Coefficiente di determinazione
- Correlazione spuria
- Covarianza (probabilità)
- Indice di correlazione di Pearson
- Regressione lineare
- Variabile (statistica)
Altri progetti
[modifica | modifica wikitesto] Wikizionario contiene il lemma di dizionario «correlazione»
Wikizionario contiene il lemma di dizionario «correlazione» Wikiversità contiene risorse sulla correlazione
Wikiversità contiene risorse sulla correlazione Wikimedia Commons contiene immagini o altri file sulla correlazione
Wikimedia Commons contiene immagini o altri file sulla correlazione
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) correlation, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Statistical Correlation, su MathWorld, Wolfram Research.
| Controllo di autorità | Thesaurus BNCF 15575 · LCCN (EN) sh85033032 · GND (DE) 4165343-9 · BNF (FR) cb11978503n (data) · J9U (EN, HE) 987007567883105171 |
|---|







